Мезоскопическое несоответствие — новый взгляд на эпитаксию наноструктур

Сегодня, после более чем ста лет активных исследований на предмет напряжений и деформаций на поверхностях, идея о том, что последние играют решающую роль в определении динамики морфологии и роста, как поверхности, так и находящихся на них наноструктур, кажется почти тривиальной. Например, пониженная координация поверхностных атомов, которая может приводить к сокращению межатомных расстояний и реконструкции поверхности, проявляется в ещё более явном виде для наноструктур на поверхности, вызывая в них и в подложке сложные и высокоанизотропные поля деформаций.

В настоящее время под обобщающим названием «мезоскопическое несоответствие» (mesoscopicmisfit) принято понимать деформации поверхности и наноструктур на них, вызванные многочисленными эффектами, связанными с конечными размерами системы или принципиальным несовпадением параметров решётки составляющих её материалов [1]. В опубликованной нами статье проведена попытка объединить результаты и внести некоторый порядок в современное понимание того, как и когда возникает мезоскопическое несоответствие в наноструктурах на металлических поверхностях и какое оно оказывает воздействие на морфологию, рост, электронные и магнитные свойства системы. С развитием концепции мезоскопического несоответствия сегодня стало очевидным его влияние в масштабах длинны от сотен нанометров до нескольких ангстрем. Этот диапазон мы будем иметь ввиду, говоря «мезоскопический», хотя для большей части обсуждаемых эффектов он может быть сужен до пределов от единиц до десятков нанометров.

Несмотря на то, что наше современное понимание возможных истоков теории мезоскопического несоответствия пока нельзя считать полным, сама идея о том, что напряжения и деформации поверхности играют фундаментальную роль в определении свойств последней, была высказана более века назад в работах Гиббса. В начале 20-го века, в период интенсивного развития кристаллографии,когда впервые один кристаллический материал был выращен на поверхности другого (процесс, для которого термин «эпитаксия» был введён Руайе),напряжение на границе раздела кристаллических материалов обычно рассматривалось как результат только «естественного несоответствия» (на основе различия постоянных кристаллической решётки двух материалов). Понимание того, что напряжение является мерой избыточности, которую поверхность будет стремиться устранить, чтобы минимизировать свою энергию, потребовало хорошей предсказательной теории, способной достаточно точно учесть влияние напряжения и деформаций на величину поверхностной энергии. На основании определений напряжения и деформации, данных Гиббсом, Шаттлуортом, Херрингом и др., было разработано их последовательное теоретическое описание для поверхностей, показывающее, что, среди прочего, они могут быть сильно анизотропными и неоднородными.

В конце 1920-х Леннард-Джонс и Дент выдвинули три замечательных утверждения: (I) физика атомных масштабов может привести к равновесному сокращению длин связей на поверхности кристалла; (II) нормальная к поверхности кристалла составляющая результирующего напряжения приводит к сокращению межслоевых расстояний вблизи поверхности; (III) несоответствие между равновесными длинами связи на поверхности и в объёме кристалла приводит к тому, что поверхность подвергается растягивающему напряжению. Эти три утверждения оказались исключительно оригинальными для того времени и стали, вероятно, одной из первых попыток атомистического описания поверхностных напряжений и деформаций. Основополагающей стала работа Полинга, в которой на основе квантовомеханических соображений был установлен набор более общих правил, относящихся к связям посредством электронных пар, в частности, касающихся прочности связей в зависимости от природы одноэлектронных собственных функций. Одно общее утверждение, которое следует из этих правил и будет для нас особенно важным, может быть выражено в следующей простой формулировке — чем меньше связей у атома, тем сильнее каждая из них.

В 1950-е годы, когда эксперименты по дифракции электронов с высоким разрешением доказали, что, вне всякого сомнения, сжатие решётки в мелких металлических кристаллах действительно происходит и, более того, зависит от их размера, теоретическое предсказание, выдвинутое Леннардом-Джонсом, Дентом и Полингом, стало преобладающим объяснением такого рода экспериментальных наблюдений. Достоверное экспериментальное определение сжатия решётки также позволило получать значения поверхностного напряжения для различных материалов.

Благодаря появлению в 1990-е годы локальных зондовых методов (таких как сканирующая туннельная микроскопия — STM), позволяющих исследовать свойства поверхности в реальном атомном масштабе, стало ясно, что как возникновение мезоскопического несоответствия, так и возможные его последствия были ещё далеко не полностью оценены. Было замечено, что даже атомы лёгких элементов при адсорбции на поверхность могут вызывать сложные сдвиги окружающих поверхностных атомов. Данный результатнамекал на то, что свойства связи на атомном уровне играют ключевую роль в определении локальных сил и, следовательно, морфологии системы. Так STM-измерения продемонстрировали, что конкуренция между поверхностными и объёмными напряжениями (так называемые деформационные релаксации) может привести к росту разветвлённых островковна начальной стадии эпитаксии меди на поверхности Ni(001) или к эффекту формирования островков правильной формы при высокой температуре.

Важнейшие идеи пришли также из теоретических работ. Концепция мезоскопического несоответствия строилась и разрабатывалась для устранения недостатков континуальной теории упругости, которая долгое время была фактически основной в описании искажений границ раздела.В классической континуальной теории снятие напряжений описывается на основе «макроскопического» или естественного несоответствия решёток m0=(aads–as)/aads, где aads и as — равновесные длины связи материалов адсорбата и поверхности; соответственно, если m0 > 0 (m0 < 0), несоответствие приводит к сжатию(растяжению) адсорбированной структуры. Однако, если адсорбированная система имеет «мезоскопические» размеры (в несколько сотен атомов или меньше), действительные длины связей в ней сильно отличаются от длин связей в объёмах соответствующих кристаллов. Неоднородная в пространстве зависимость длин межатомных связей от масштаба атомных длин приводит к мезоскопическому несоответствию, которое возникает в структурах конечных размеров, варьируется в субнанометровом масштабе (в зависимости не только от естественного несоответствия, но и от локального окружения конкретных атомов) и часто приводит к сложным трёхмерным полям деформаций как в адсорбированной структуре, так и в подложке [1]. Даже при гетероэпитаксии, которая считалась хорошо изученной в рамках континуальной теории упругости, некоторые эффекты невозможно было понять без рассмотрения несоответствия как существенно локального, мезоскопического свойства системы. Например, если растягивающее напряжение можно ожидать в рамках естественного несоответствия в таких системах как Fe, Co, Ni и Cu на поверхности W(110) в режиме роста субмонослоя, то по факту сжимающее напряжение было обнаружено экспериментально для таких гетероэпитаксиальных систем. Более неожиданным было наблюдение внутриплоскостных осцилляций параметра решётки, обнаруженных методом дифракции быстрых электронов (RHEED) при эпитаксии кобальта на поверхности Cu(001) в режиме псевдоморфного роста: в растущих моноатомных слоях кобальта происходило периодическое «поджатие» для полуцелых покрытий поверхности [2]. Поэтому одновременно с экспериментальными измерениями проходили и теоретические изыскания с целью улучшения макроскопического подхода континуальной теории упругости для описания первых стадий эпитаксиального роста.Керн и Мюллер выступили за использование так называемого «активного несоответствия» — поправки к естественному несоответствию, учитывающей пониженную координацию атомов на краях наноструктуры [3]. Главная идея заключалась в том, что атомы на краях наноструктуры будут стремиться к релаксации своих позиций, чтобы увеличить энергию своих связей путём максимизации числа ближайших соседей.

Основополагающие работы по развитию концепции мезоскопического несоответствия появились лишь в начале 2000-х годов. Первые ключевые расчёты были проведены нашей группой на основе разработанной нами уникальной методики, получившей название квази-первопринципной молекулярной динамики с применением усовершенствованных многочастичных потенциалов [4,5]. Результаты наших исследований впервые показали, что, во-первых, не только напряжения и деформации в адсорбированной структуре определяют её форму и механизм роста, но и деформация подложки является механизмом снятия напряжений в ней, оказывая порой решающее воздействие на процесс эпитаксии и его энергетику. Во-вторых, было показано, что напряжения и деформации сильно зависят от локального окружения (т. е. от формы и размера адсорбированной наноструктуры). Таким образом, наконец, была однозначно установлена первостепенная важность «локального» или «мезоскопического» подхода к несоответствию, в противоположность опирающемуся, в духе континуальной теории упругости, на объёмные макроскопические значения естественного несоответствия. В-третьих, что не менее важно, мезоскопическое несоответствие не должно являться исключительным свойством гетероэпитаксиальных систем, но должно также существовать и в гомоэпитаксиальных системах — утверждение, позднее доказанное экспериментально и обобщившее понятие мезоскопического несоответствия для произвольной системы, независимо от её химического состава.

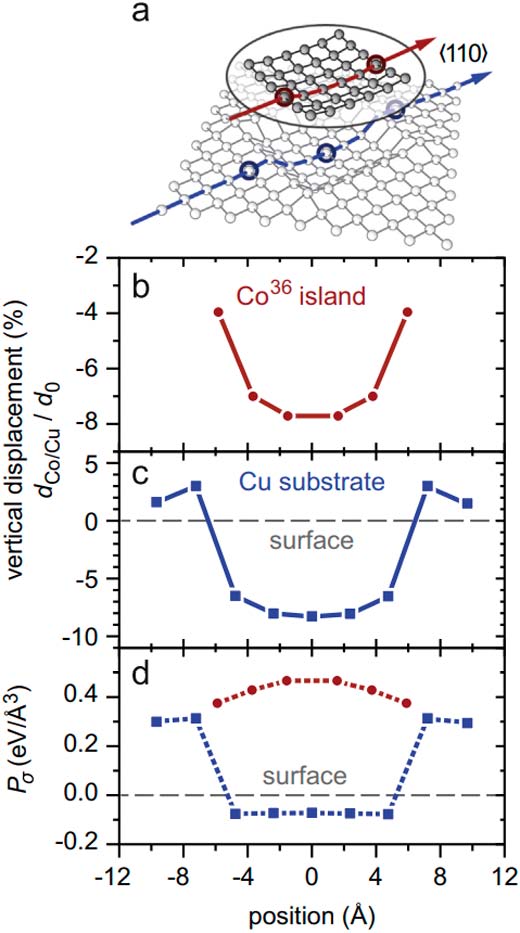
В качестве иллюстративного примера мезоскопического несоответствия и деформационных релаксаций в эпитаксиальных наноструктурах на Рис. 1 показаны смещения атомов в островке Co36 и в прилегающем участке подложки вдоль направления (110) поверхности Cu(001) [5]. Из рисунка видно, что помимо выраженных внутриплоскостных релаксаций в системе видны сильные внеплоскостные смещения. Атомы подложки под островком вдавлены вниз, в то время как по краям островка они приподняты. Среднее относительное смещение (определяемое из анализа длин связей) в слое подложки под кластером в плоскости поверхности отрицательно, то есть атомная структура подложки находится под действием напряжения сжатия. Описанные релаксационные эффекты были также установлены в структурах Co на Cu(111), убедительно показа в общую применимость концепции мезоскопического несоответствия к различным структурам, сформированным на ранних стадиях эпитаксии тонких плёнок. Кроме того, на основе проведенных расчетов был впервые предоставлен доступ к локальной (атомного уровня) картине напряжений и деформаций, который даже современные экспериментальные методы не могут пока обеспечить в достаточной степени. Так на Рис. 1(d) показано атомарно разрешённое гидростатическое напряжение P? = Tr(???) в островках Co36 и в поверхностном слое Cu [5]. Как видно из рисунка, атомный слой меди вблизи края островка испытывает сильное растягивающие (положительное) напряжение, в то время как слой подложки под островком испытывает сжимающее (отрицательное)

Рис. 1. (a) Эскиз системы (квадратный островок Co36 на поверхности Cu(001)) и трёхмерное представление релаксаций. (b) Вертикальное смещение атомов кобальта в островке и (c) атомов меди в верхнем слое подложки вдоль направления (110). Расстояние между слоями d0= 1,8075 ?, постоянная решётки меди a0= 3,615 ?. (d) Гидростатичес-кое напряжение в том же островке и слое подложки [5].

гидростатическое напряжение. Различное растягивающее напряжение наблюдаетсяв центре и на краю кластера, что указывает на необходимость рассматривать несоответствие с мезоскопической, а не с макроскопической точки зрения.

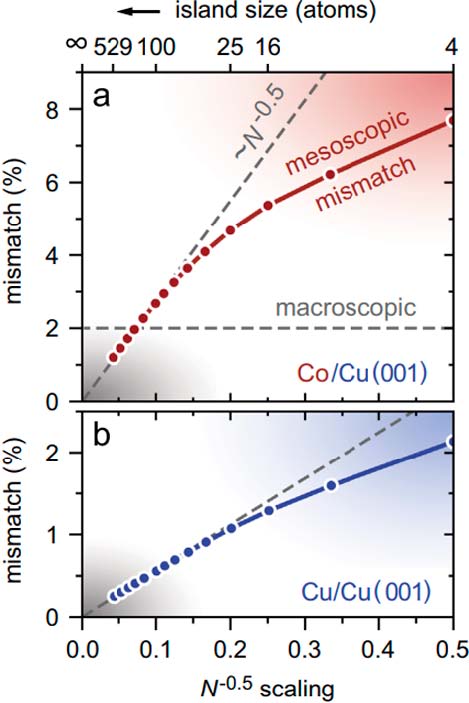
Однако более важным оказалось то, что гомоэпитаксиальные структуры также подвержены закономерностям при деформационных релаксациях, которые во многом схожи со случаем гетероэпитаксии [1]. Этот результат бросал вызов общепринятому представлению о согласованности решёток островка и подложки в рамках классического континуально-упругого подхода к гомоэпитаксии, мотивируя необходимость перехода к более полной мезоскопической картине несоответствия. В качестве иллюстрациина Рис. 2 мы представляем пример расчёта мезоскопического несоответствия в квадратных островках кобальта и меди моноатомной толщины на поверхности Cu(001) в зависимости от их размеров как средней длины связи в таких кластерах с учётом полной релаксации системы [6]. Мезоскопическое несоответствие при этом определялось как m=(rb–r0)/r0 (rb и r0 — средние длины связей, соответственно, в островке и в объёме медного кристалла). Видно, что между небольшими островками кобальта и медной подложкой (гетероэпитаксиальная система) оно заметно больше, чем макроскопическое m0=(aCo–aCu)/aCo?0,02 (где aCu и aCo — характерные размеры длин связей в кристаллах меди и кобальта), и отлично от нуля для медных островков (гомоэпитаксиальная система).

Рис. 2. Эволюциясреднего мезоскопического несоответствия m=(rb–r0)/r0 для квадратных островков кобальта (a) и меди (b) как функции размера островка N (число атомов, растет справа налево). rb и r0 — средние длины связей, соответственно, в островке и в объёме медного кристалла [6].

Это связано с тем, что средняя длина связи в островках меньше, чем в объёме ГЦК-кристалла меди, что полностью противоречит интуитивному представлению с точки зрения континуальной теории упругости. Такое сжатие обусловлено сильным смещением краевых атомов и частично внутренних атомов в результате их релаксации (как видно на Рис. 1). С ростом размера островков несоответствие масштабируется в соответствии с долей атомов, принадлежащих их краям, и зависимость становится пропорциональной N-0,5 (серые пунктирные линии на Рис. 2).

Таким образом, мезоскопическое несоответствие не только является сильно зависящим от размеров наноструктуры, но и, как будет показано ниже, само, в свою очередь, влияет на морфологию и динамику роста эпитаксиальной наноструктуры.

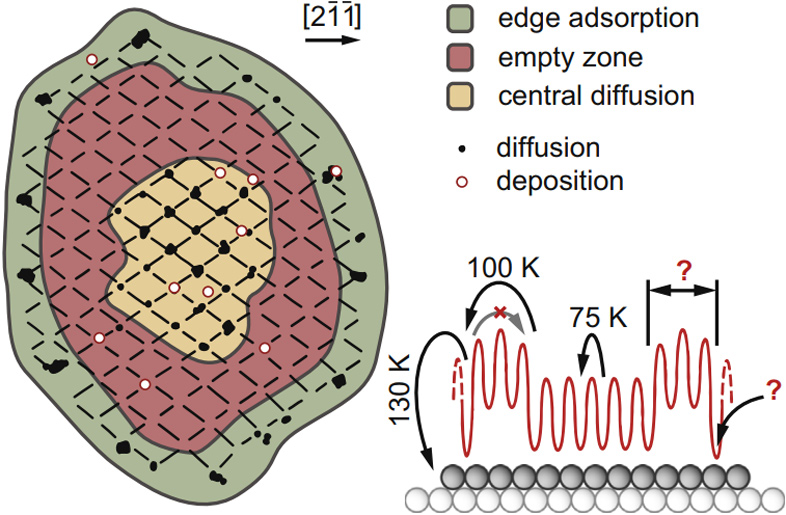
Попытка прямого наблюдения динамики роста адатомов на поверхности островков была впервые предпринята в экспериментах полевой ионной микроскопии (FIM) Эрлихоми Гольцхаузером [7]. Эти эксперименты продемонстрировали, что движение адатомов на вершинах островков отличается от их движения по ровной поверхности. При диффузии иридия на поверхности Ir(111) и платины на поверхности Pt(111) была обнаружена «оголённая» зона, разделяющая центральную область и край кластера (Рис. 3).

Эта «загадка» впоследствии была разгадана нами с помощью уникальной методики расчетов на атомном уровне, которые показали, что эффект пустых зон является следствием тонкого баланса между деформационными релаксациями в системе и уменьшением координационного числа на краях кластеров с образованием невыгодной зоны адсорбции, разделяющей центральную и краевую части островков [1]. В результате отдельным атомам приходится преодолевать энергетический барьер, чтобы пересечь пустую зону и достигнуть края кластера.Более детальное исследование влияния напряжений на подвижность отдельных атомов по поверхности деформированных Co-островков на Cu(001) показало, что на данное движение сильное влияние оказываютне только деформационные релаксации на мезоскопическом уровне, но и размер самих островков [6]. Барьеры прыжковой диффузии атомов кобальта на поверхностях небольших Co-островков (16-50 атомов) оказались на ~20% ниже, чем на более крупных островках (100-500 атомов). Мезоскопическое сокращение связей, зависящее от размеров островков, явилось главной причиной изменения диффузионных барьеров на их поверхностях. Более плотная упаковка последних уменьшает «волнистость» энергетического

Рис. 3. Отображениепозиций, занимаемых атомами Pt на кластере Pt(111) из ~145 атомов. Закрашенными метками отмечены положения атомов после диффузии. Пустые метки обозначают атомы после осаждения при ~20 K. Только один атом находится на кластере в каждый определённый момент при отображении. «Оголённую» зону, отделяющую центральную область от края кластера, могут заселять атомы при осаждении. Схема в правой нижней части демонстрирует адсорбционный потенциал на поверхности островка и температуру, при которой задействуются определённые процессы транспорта [7].

рельефа, что делает движение адсорбированных атомов более свободным.

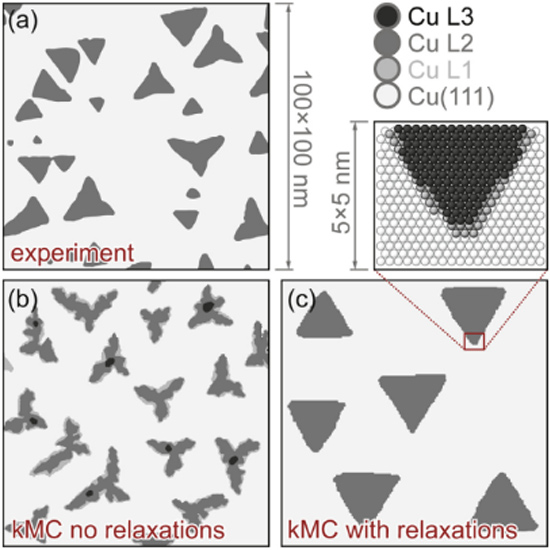
Важным следствием таких изменений может быть прямое воздействие на эпитаксиальный рост. Так, впервые объединив кинетический метод Монте-Карло (kMC) и молекулярно-статическое моделирование в атомном масштабе, нам удалось обнаружить формирование треугольных двухслойных островков кобальта на поверхности Cu(111) при комнатной температуре, сравнив полученные нами результаты с экспериментальными наблюдениями [1]. Согласно последним, при 290 K кобальт, осаждённый в 0,4 монослоя на поверхность Cu(111), образует вполне разделённые треугольные островки правильной формы (Рис. 4(a)). Принимая во внимание все соответствующие процессы атомного уровня, но пренебрегая мезоскопическими релаксациями в системе, kMC-моделирование предсказывает совершенно иную, дендритную структуру островка (Рис. 4(b)), характерную для гораздо более низких температур в эксперименте.

Рис. 4. Поверхность Cu(111) с осаждённым в 0,4 монослояпри 290 K кобальтом: эксперимен-тальная STM-карта (a) и результат kMC-моделирования без деформационных релаксаций (b)и с правильным их учётом (c) [1].

Однако, как только в модель вводятся мезоскопические эффекты (Рис. 4(c)), образующиеся формы островков почти идеально соответствуют экспериментальным.

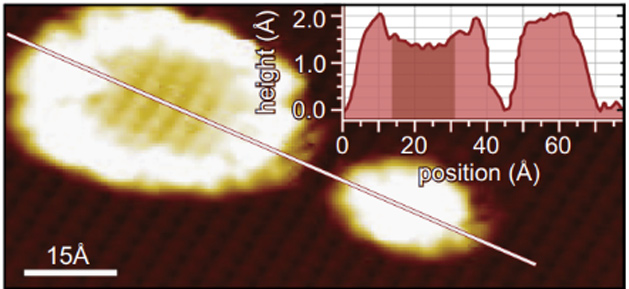
В последнее десятилетие многочисленные теоретические и экспериментальные исследования были направлены на то, чтобы в деталях понять и увидеть, как именно возникает мезоскопическое несоответствие. На сегодняшний день можно отметить лишь несколько наиболее важных прямых экспериментальных подтверждений мезоскопического несоответствия, которые были достигнуты с развитием в последние годы экспериментально-технической базы. Первое из них основано на комбинации метода дифракциирентгеновских лучей на поверхности (SXRD) и STM-измерений [8]. STM-изображение поверхностной атомной структуры, образованной 0,5 монослоя железа на O/Fe(001)–p(1?1), в режиме постоянного тока на Рис. 5 даёт доказательство того, что размерный эффект играет главную роль в модификации геометрии адсорбции кислорода в этой системе. На большом островке железа диаметром 4 нм видны две области: (i) со структурой окружающей его террасы — во внутренней части и (ii) с повышенным контрастом и потерей атомарного разрешения — на «краю» островка (шириной ?1 нм), соответствующая наблюдаемому возвышению на 0,75 ? над внутренней частью островка.

Высотный профиль вдоль линии показывает, что малый островок и краевая структура большого островка железа имеют одинаковую видимую высоту ?2 ? относительно уровня террасы. В рамках второго подхода для подтверждения существования мезоскопических релаксаций были проведены исследования поверхности Cu(001) при малом покрытии кобальтом (< 1 монослоя) методом EXAFS (протяжённой тонкой структуры рентгеновского спектра поглощения) [9]. В результате экспериментального анализа и теоретического расчета преобразования Фурье интерференционной функции спектров EXAFS были получены два замечательных результата: во-первых, однозначное свидетельство сокращения межатомных Co-Co расстояний

Рис. 5. STM-изображение в режиме постоянного тока (8,0 ? 3,6 нм2, напряжение смещения –0,2 В, I = 100 пА) двух Fe-островков (? ? 20 и 35 ?) [8]. На вклейке показан видимый высотный профиль вдоль линии.

c RCo = 2,51 ? в объеме до RCo = 2,45 ± 0,02 ? в островке кобальта. Во-вторых, эффективное (среднее) координационное число атомов кобальта в островке уменьшено с NCo = 6,0 (для бесконечно большого островка) до NCo = 3,2. Эти результаты соответствуют нашим теоретическим предсказаниям и могут рассматриваться как прямое доказательство существования структурных релаксаций, вызванных мезоскопическим несоответствием.

Подводя итоги, можно сказать, что мезоскопическое несоответствие оказывает сильное воздействиена структуру поверхности, а также влияет на динамику роста и морфологию эпитаксиальных структур на ней. На протяжении последних лет предметом подробного исследования были различные способы, которыми несоответствие может оказывать такое влияние. Сокращение длин связей, внутри- и внеплоскостные релаксации на краях, преобразование формы в зависимости от размера структуры — вот лишь некоторые из них. Во всех этих проявлениях можно проследить влияние несоответствия в истинно атомном масштабе на такие элементарные процессы, как атомная адсорбцияи диффузия. Однако, они не являются единственными индикаторами влияния мезоскопического несоответствия на свойства эпитаксиальных наноструктур. В настоящее время установлено, что деформационные релаксации в равной мере оказывают влияние на электронные и магнитные свойства, что проявляется в таких свойствах наноструктур, как локальные магнитные моменты, магнитная анизотропия и электронная структура [10].

В заключение хотелось бы отметить, что важнейшее преимущество теоретического подхода к исследованию проблемы мезоскопического несоответствия состоит в том, что большинство экспериментальных методов способны обнаружить лишь последствия этого несоответствия, в то время как теоретические методы на основе первопринципных и полуэмпирических расчётов способны дать локальную, разрешённую на атомном уровне картину геометрических, электронных и магнитных свойств системы, оставляя мало места для ошибок и неверных интерпретаций.

[1] O.O. Brovko, D.I. Bazhanov, H.L. Meyerheim, D. Sander, V.S. Stepanyuk, J. Kirschner, Surf. Sci. Rep. 69, 159 (2014).

[2] D. Sander, R. Skomski, C. Schmidthals, A. Enders, J. Kirschner, Phys. Rev. Lett. 77 (12), 2566 (1996); J. Fassbender, U. May, B. Schirmer, R. Jungblut, B. Hillebrands, G. G?ntherodt, Phys. Rev. Lett. 75 (24), 4476 (1995).

[3] R. Kern, P. M?ller, Surf. Sci. 392 (1–3), 103 (1997).

[4] N. Levanov, V. Stepanyuk, W. Hergert, D. Bazhanov, P. Dederichs, A. Katsnelson, C. Massobrio, Phys. Rev. B 61 (3),2230 (2000).

[5] V.S. Stepanyuk, D.I. Bazhanov, A.N. Baranov,

W. Hergert, P. Dederichs, J. Kirschner, Phys. Rev.

B 62 (23),15398 (2000).

[6] V. Stepanyuk, D. Bazhanov, W. Hergert, J. Kirschner,

Phys. Rev. B 63 (15), 153406 (2001).

[7] A. G?lzh?user, G. Ehrlich, Phys. Rev. Lett. 77 (7),

1334 (1996).

[8] W. Feng, H.L. Meyerheim, K. Mohseni, O.O. Brovko,

V.S. Stepanyuk, N. Jedrecy, R. Felici, J. Kirschner,

Phys. Rev. Lett. 110 (23), 235503 (2013).

[9] H.L. Meyerheim, E. Crozier, R. Gordon, Q. Xiao,

K. Mohseni, N. N. Negulyaev, V.S. Stepanyuk,

J. Kirschner, Phys. Rev. B 85 (12),125405 (2012).

[10] D. Sander, S.-H. Phark, M. Corbetta, J. Fischer, H. Oka,

J. Kirschner, J. Phys.: Condens. Matter 26, 394008 (2014).

Бажанов Д.И., кафедра физики твердого тела